Boolesche Algebra: Unterschied zwischen den Versionen
(→De Morgansche Gesetze) |
|||
| Zeile 172: | Zeile 172: | ||
Alltagsbeispiel: | Alltagsbeispiel: | ||
| − | Peter trinkt Tee nur mit Zitronensaft und Zucker. | + | Peter trinkt Tee nur mit Zitronensaft und Zucker. |
| − | + | Beschreibe die Boolesche Variable '''A''' den Zustand, dass Zucker im Tee ist und '''B''' den Zustand, dass sich Zitronensaft im Tee befindet. Dann lautet die Antwort auf die Frage, ob Peter Tee mit Zucker und Zitronensaft trinken wird mit Hilfe der Variablen '''A''' = '''true''', '''B''' = '''true''' (denn sowohl Zitronensaft als auch Zucker sind im Tee): | |
| − | + | ||
| + | ¬(''A'' ∧ ''B'') = ¬(''true'' ∧ ''true'') = ¬''true'' =''false'' (Peter trinkt den Tee nicht) | ||
| + | |||
| + | und diese ist offensichtlich die gleiche Antwort wie auf die Frage, ob Peter Tee trinken würde, wenn kein Zitronensaft oder kein Zucker im Tee wäre (also wenigstens eine der gewünschten Zutaten fehlt) | ||
| + | |||
| + | ¬''A'' ∨ ¬''B'' = ¬''true'' ∨ ¬''true'' = ''false'' ∨ ''false'' = false. | ||
| + | |||
| + | |||
| + | Peters Freundin Petra mag ihren Kaffee nicht schwarz, er muss wenigstens Milch oder Zucker enthalten. Die Variable '''A''' beschreibende den Zustand, dass der Kaffee Milch enthält und '''B''', dass Zucker enthalten ist. | ||
| + | Trinkt Petra ihren Kaffee nicht, wenn Peter ihn mit Milch aber ohne Zucker zubereitet? | ||
| + | |||
| + | ¬(''A'' ∨ ''B'') =¬(''true'' ∨ ''false'') = ¬''true'' = ''false'' (es ist also falsch, dass Petra den Kaffee nicht trinkt) | ||
| + | |||
| + | und das gleiche Ergebnis ergibt sich für die Variante ohne Milch aber mit Zucker | ||
| + | |||
| + | ¬''A'' ∧ ¬''B'' = ¬''true'' ∧ ¬''false'' = ''false'' ∧ ''true'' = ''false''. | ||
===Komplementärgesetze=== | ===Komplementärgesetze=== | ||
Version vom 4. September 2016, 17:35 Uhr
Die boolesche Algebra ist eine algebraische Struktur und beschreibt die Operationen UND, ODER und NICHT, die auf logische Aussagen angewendet werden können. Die Kenntnis dieser Struktur ist hilfreich für den Umgang mit dem Datentyp boolean.
Inhaltsverzeichnis
Die booleschen Operatoren
Konjunktion (AND)
Die Konjunktion ist eine der grundlegenden logischen Verknüpfungen der Aussagenlogik. Die Konjunktion zweier Aussagen A und B ist genau dann wahr, wenn A und B (sowohl als auch) wahr sind. Das mathematische Symbol ist ∧. In Java wird das AND durch && repräsentiert.
| A | B | A ∧ B |
|---|---|---|
| false | false | false |
| false | true | false |
| true | false | false |
| true | true | true |
Disjunktion (OR)
Die Disjunktion ist eine der grundlegenden logischen Verknüpfungen der Aussagenlogik. Die Disjunktion zweier Aussagen A und B ist genau dann wahr, wenn mindestens eine der Aussagen A oder B wahr ist. Das mathematische Symbol ist ∨. In Java wird das OR durch || repräsentiert.
| A | B | A ∨ B |
|---|---|---|
| false | false | false |
| false | true | true |
| true | false | true |
| true | true | true |
Venn-Diagramm?
Negation (NOT)
Die Negation ist eine wichtige Operation in der Aussagenlogik. Die Negation einer Aussage A führt zur ihrer Verneinung. Das heißt aus einer wahren Aussage wird eine falsche Aussage und umgekehrt. Das mathematische Symbol ist ¬. In Java wird das NOT durch ! repräsentiert.
| A | ¬A |
|---|---|
| false | true |
| true | false |
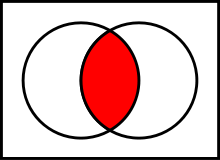
Kontravalenz (XOR)
Die Kontravalenz ist eine erweiterte logische Verknüpfung in der Aussagenlogik. Die Kontravalenz zweier Aussagen A und B ist genau dann wahr, wenn entweder A oder B, aber nicht beide wahr sind. Das mathematische Symbol ist ⊕. In Java wird das XOR durch ^ repräsentiert.
| A | B | A ⊕ B |
|---|---|---|
| false | false | false |
| false | true | true |
| true | false | true |
| true | true | false |
Venn-Diagramm?
Implikation
Die Implikation ist eine erweiterte logische Verknüpfung in der Aussagenlogik. Die Implikation zweier Aussagen A und B ist genau dann wahr, wenn A falsch oder B wahr ist. Das mathematische Symbol ist ⇒. Die Implikation ist semantisch äquivalent zu ¬A ∨ B. In Java gibt es keinen Implikationsoperator.
Eine Implikation wird im Deutschen meistens durch "wenn A, dann B" ausgedrückt. Es handelt sich hierbei um eine einfache Folgerung. Aus einer falschen Ausgangsaussage A lässt sich alles folgern, daher kann die Gesamtaussage nicht falsch werden.
| A | B | A ⇒ B |
|---|---|---|
| false | false | true |
| false | true | true |
| true | false | false |
| true | true | true |
Venn-Diagramm?
Äquivalenz (XNOR)
Die Äquivalenz ist eine erweiterte logische Verknüpfung in der Aussagenlogik. Die Äquivalenz zweier Aussagen A und B ist genau dann wahr, wenn A und B wahr oder A und B falsch sind. Das mathematische Symbol ist ⇔. Die Äquivalenz ist semantisch äquivalent zu A ∧ B ∨ ¬A ∧ ¬B. In Java gibt es keinen Operator hierfür.
Die Äquivalenz wird im Deutschen meistens durch "genau dann A, wenn B" ausgedrückt. "Genau" heißt immer und nur unter dieser Bedingung. A gilt genau dann, wenn B gilt. A und B sind äquivalent, also austauschbar. Das heißt die vorherige Aussage gilt auch anders herum: B gilt genau dann, wenn A gilt.
| A | B | A ⇔ B |
|---|---|---|
| false | false | true |
| false | true | false |
| true | false | false |
| true | true | true |
Venn-Diagramm?
Peano-Axiome (erweitertes Wissen)
Kommutativgesetze
(1) A ∧ B ≡ B ∧ A
(1') A ∨ B ≡ B ∨ A
Das Vertauschen der Argumente A und B ist hier möglich, ohne dass sich das Ergebnis der Operation ändert.
Assoziativgesetze
(2) (A ∧ B) ∧ C ≡ A ∧ (B ∧ C)
(2') (A ∨ B) ∨ C ≡ A ∨ (B ∨ C)
Die Klammerung der oben durchgeführten Operationen hat keinen Einfluss auf das Ergebnis.
Idempotenzgesetze
(3) A ∧ A ≡ A
(3') A ∨ A ≡ A
Die Eigenschaften des Arguments A bleiben bestehen, auch wenn dieses mit sich selbst verknüpft wird.
Distributivgesetze
(4) A ∧ (B ∨ C) ≡ (A ∧ B) ∨ (A ∧ C)
(4') A ∨ (B ∧ C) ≡ (A ∨ B) ∧ (A ∨ C)
Auswirkung des Auflösens von Klammern um Verknüpfungen von Operationen; ähnlich dem "Ausmultiplizieren" in der Schulmathematik.
Neutralitätsgesetze
(5) A ∧ true ≡ A
(5') A ∨ false ≡ A
Der Wert des Argumentes A wird durch die oben ausgeführten Operationen nicht verändert.
Extremalgesetze
(6) A ∧ false ≡ false
(6') A ∨ true ≡ true
Das Ergebnis der oben beschriebenen Operationen ist unabhängig vom Wert des Arguments A.
Doppelnegationsgesetz
(7) ¬(¬A) ≡ A
"Doppelte Verneinung": Der Wert von A wird durch zweimaliges Ausführen des ¬ -Operators nicht beeinflusst.
De Morgansche Gesetze
(8) ¬(A ∧ B) ≡ ¬A ∨ ¬B
(8') ¬(A ∨ B) ≡ ¬A ∧ ¬B
Alltagsbeispiel:
Peter trinkt Tee nur mit Zitronensaft und Zucker. Beschreibe die Boolesche Variable A den Zustand, dass Zucker im Tee ist und B den Zustand, dass sich Zitronensaft im Tee befindet. Dann lautet die Antwort auf die Frage, ob Peter Tee mit Zucker und Zitronensaft trinken wird mit Hilfe der Variablen A = true, B = true (denn sowohl Zitronensaft als auch Zucker sind im Tee):
¬(A ∧ B) = ¬(true ∧ true) = ¬true =false (Peter trinkt den Tee nicht)
und diese ist offensichtlich die gleiche Antwort wie auf die Frage, ob Peter Tee trinken würde, wenn kein Zitronensaft oder kein Zucker im Tee wäre (also wenigstens eine der gewünschten Zutaten fehlt)
¬A ∨ ¬B = ¬true ∨ ¬true = false ∨ false = false.
Peters Freundin Petra mag ihren Kaffee nicht schwarz, er muss wenigstens Milch oder Zucker enthalten. Die Variable A beschreibende den Zustand, dass der Kaffee Milch enthält und B, dass Zucker enthalten ist.
Trinkt Petra ihren Kaffee nicht, wenn Peter ihn mit Milch aber ohne Zucker zubereitet?
¬(A ∨ B) =¬(true ∨ false) = ¬true = false (es ist also falsch, dass Petra den Kaffee nicht trinkt)
und das gleiche Ergebnis ergibt sich für die Variante ohne Milch aber mit Zucker
¬A ∧ ¬B = ¬true ∧ ¬false = false ∧ true = false.
Komplementärgesetze
(9) A ∧ ¬A ≡ false
(9') A ∨ ¬A ≡ true
Es können nicht gleichzeitig A und die Negation von A gelten: Beispielsweise kann der Himmel nicht gleichzeitig blau und nicht-blau sein (9). Allerdings ist der Himmel entweder blau oder nicht-blau gefärbt (9').
Dualitätsgesetze
(10) ¬false ≡ true
(10') ¬true ≡ false
Der Wert true ist das Komplement zu false. Ist eine Aussage nicht-wahr, so ist sie falsch. Umgekehrt gilt für eine nicht-falsche Aussage, dass sie wahr sein muss.